Turing Machine

In this example, we show how we can simulate a Turing machine purely within the dataflow graph language of OptFlow. In such a way we prove that the dataflow graph language in OptFlow is Turing-complete. That is, from the perspective of computability theory, it is computationally universal to simulate the computational aspects of any possible real-world computer.

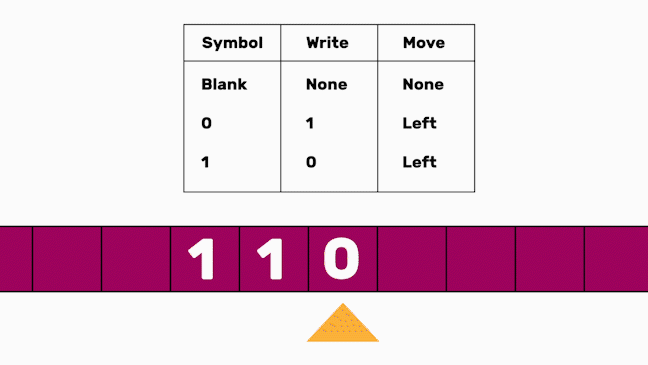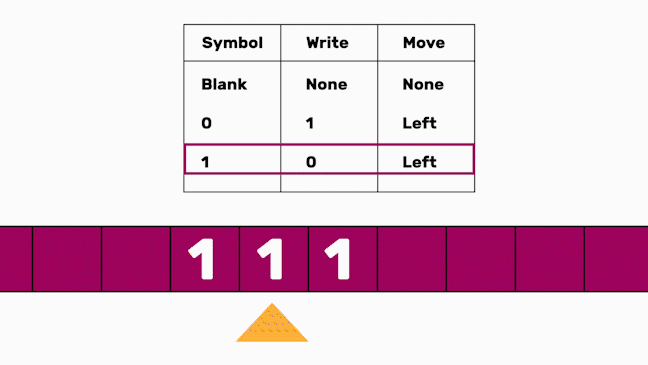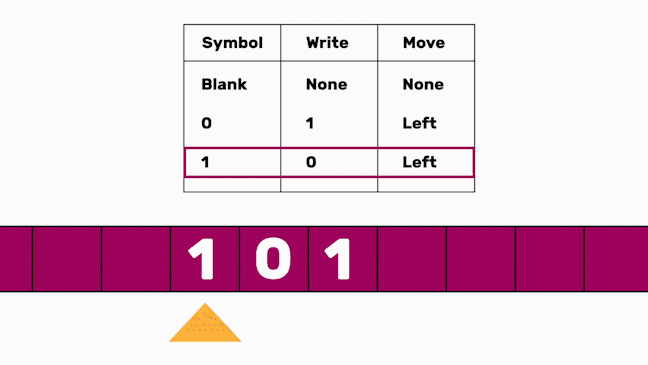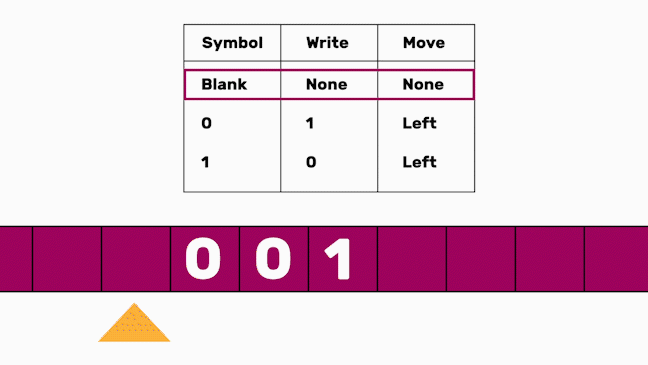
In the following code, we define a Turing machine with two states: 0 (init) and 1 (final) and an alphabet size of 2 (0 and 1). Its transition function is

state, tape_read -> next_state, tape_write, tape_move

which means “If the machine is in state state and tape_read is read by the head, a tape_write will be written, the state will change to next_state and the head will be moved one field to the position indicated by tape_move.” Check this page for a detailed introduction.

While state, tape_read, tape_write and tape_move is given in this example, we want to optimize next_state so that the sum of number on the tape can be maximized.

import optflow as flow
import numpy as np

tape_size, max_step, transition_table_size = 5, 5, 3
tape = flow.Constant(np.array([0, 1, 0, 0, 2]))

# transition table
state = flow.Constant(np.array([0, 0, 0]))
tape_read = flow.Constant(np.array([0, 1, 2]))
next_state = flow.Variable(flow.categorical, size=2, shape=(transition_table_size, ))
tape_write = flow.Constant(np.array([1, 0, 2]))
tape_move = flow.Constant(np.array([1, 1, 1]))

s = flow.Constant(0)    # current state
p = flow.Constant(0)    # read/write head position
obj = flow.Constant(0)

with flow.ForLoop(max_step) as t:
    with flow.ForLoop(transition_table_size) as i:  # iterate the transition table
        # if the current state s and the number of tape on the head position match the current table element
        with flow.IfCond((state[i] == s) & (tape_read[i] == tape[p])):
            s = next_state[i]                       # change the state
            tape[p] = tape_write[i]                 # write the tape at the head position
            with flow.IfCond(tape_move[i] == 0):    # move the read/write head: 0 -> left, 1 -> right
                p = flow.maximum(p - 1, 0)
            with flow.IfCond(tape_move[i] == 1):
                p = flow.minimum(p + 1, tape_size - 1)
    with flow.IfCond(s == 1):   # if the Turing machine reached the final state
        flow.break_loop()       # halt

prob = flow.Problem(objective=flow.reduce_sum(tape), constraints=[], sense=flow.maximize)
prob.solve(solver=flow.search)
print(next_state.optimized_value)
prob.solve(solver=flow.metaheuristics)
print(next_state.optimized_value)

[Run Online Demo] (password: )

The result is as follows

Search started
Step 2, found a feasible solution with obj 5.000000
Search finished in 9 steps, optimal objective = 5.000000
Time elapsed: 0.12 s
[0 0 0]

indicating that the Turing machine should keep staying at the init state 0 to maximize the sum of the number on its tape.