Examples

LP = Linear Programming, MIP = Mixed Integer Programming, DP = Dynamic Programming, RL = (Model-Free) Reinforcement Learning, MCTS = Monte-Carlo Tree Search

Problem	Description	Methods
Turing Machine	Optimizes the transition function of a Turing machine to maximize the sum of the value on its tape	Search
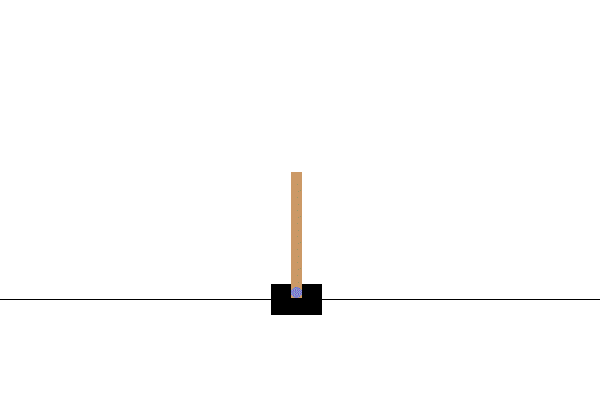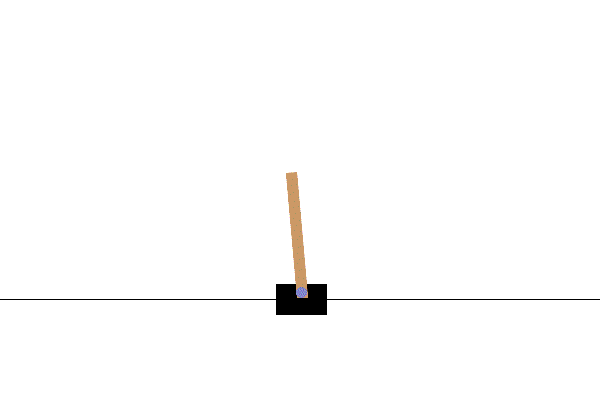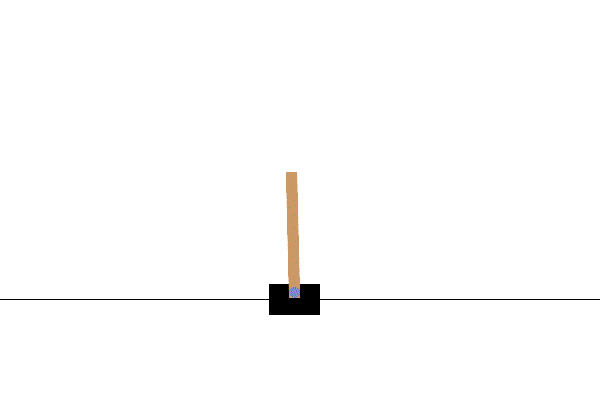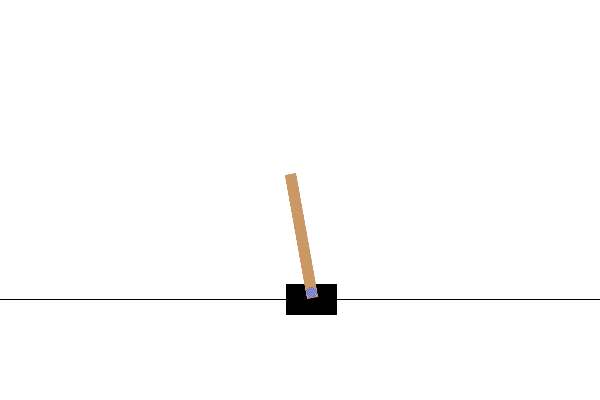
CartPole	Optimizes the action sequence of a cart to maximize the stabilization time of an inverted pendulum.	RL
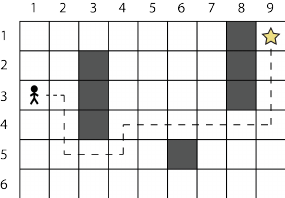
Maze	Optimizes the route of a player to escape from a maze without hitting the wall	DP, RL, Search
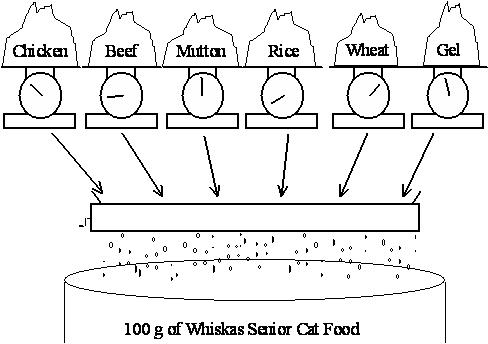
Blending Problem	Optimizes the ratio of beef and chichen to meet the nutritional standard with lowest cost	LP
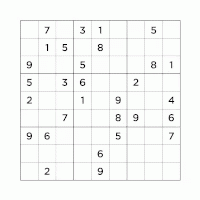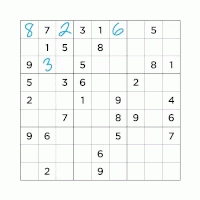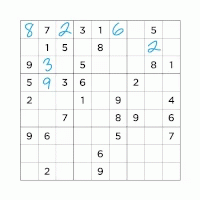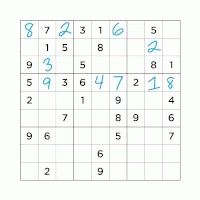
Soduku Problem	Finding a feasible solution of 9x9 Soduku	MIP
Capital Budgeting	Optimize the selection of investments to maximize the total contribution with limited availability of cash and manpower	MIP, Metaheuristics, Search, DP
Knapsack	Optimize the selection of items to maximize the total value without exceeding the capacity of the knapsack	MIP, Metaheuristics, Search, DP, RL, RL+MCTS
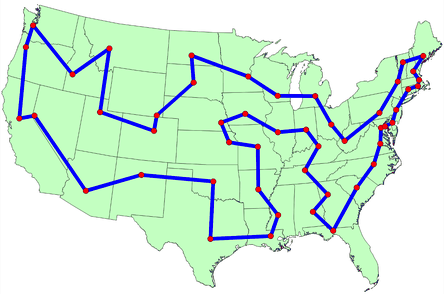
Traveling Salesman Problem	Optimize the route of a salesman that visits each city exactly once and returns to the origin city, so that the total length of the route is minimized	MIP, Metaheuristics, Search, DP, RL
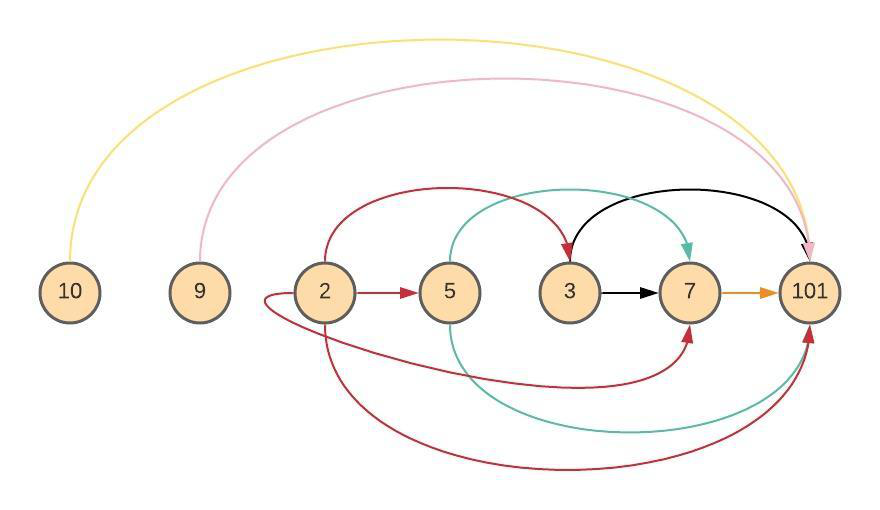
Longest Increasing Subsequence	Optimize the selection of an increasing sub-sequence from an array to maximize its length.	DP, Search
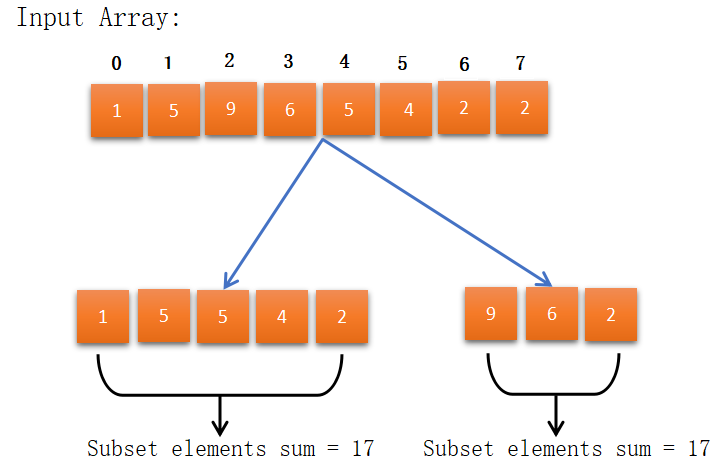
Balanced Partition	Optimize the bi-partition of an array to minimize the gap between the sum of the elements in both sets.	DP

• Turing Machine
• CartPole
• Maze
• Blending Problem
• Sudoku
• Capital Budgeting
• Knapsack Problem
• Traveling Salesman Problem (TSP)
• Longest Increasing Subsequence
• Balanced Partition